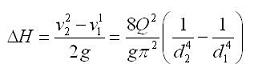КПД центробежных насосов
Гидравлическая мощность и КПД центробежных насосов
Гидравлическая мощность насоса
PГ = ρ x g x Q x H [Вт]
ρ — плотность жидкости [кг/м 3 ]
g — ускорение свободного падения [м/сек 2 ]
Q — расход [м 3 /сек]
H — напор [м]
Для насосов, у которых всасывающий и напорный патрубки имеют одинаковый диаметр и находятся на одном уровне, напор можно рассчитать по упрощённой формуле:
H = (p2 — p1) / (ρ x g) [м]
p2 — давление на напорном патрубке [Па]
p1 — давление на всасывающем патрубке [Па]
Таким образом, гидравлическая мощность насоса пропорциональна перепаду давления и расходу:
Если диаметр напорного патрубка меньше диаметра всасывающего патрубка, то для расчёта гидравлической мощности насоса напор необходимо увеличить на величину:
v2 — скорость жидкости в напорном патрубке [м/с]
v1 — скорость жидкости во всасывающем патрубке [м/с]
Q — расход [м 3 /с]
g — ускорение свободного падения [м/с 2 ]
d2 — внутренний диаметр напорного патрубка [м]
d1 — внутренний диаметр всасывающего патрубка [м]
Если напорный и всасывающий патрубок расположены не на одной линии, то напор нужно ещё увеличить на разницу высот между двумя патрубками:
Потребляемая мощность насоса
Если вал насоса жёстко соединён с валом двигателя, то потребляемая мощность насоса равна механической мощности на валу электродвигателя.
КПД насоса
КПД насоса равен отношению гидравлической мощности к потребляемой:
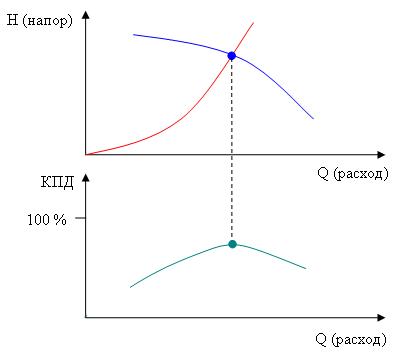
Насос выбирается так, чтобы в рабочей точке его КПД был максимальным (см. рис.).
Механическая мощность на валу электродвигателя:
ηД — КПД электродвигателя,
PЭ — электрическая мощность, потребляемая двигателем из сети.
Электрическая мощность, потребляемая 3-х фазным электродвигателем из сети
PЭ = √3 х U х I х cos φ
U — напряжение сети [В]
I — ток, потребляемый электродвигателем [А]
cos φ — косинус угла между векторами тока и напряжения
Выводы: как вычислить КПД насоса
- С помощью специального прибора с токовыми клещами измеряем электрическую мощность PЭ, потребляемую электродвигателем из сети. Если электродвигатель работает от преобразователя частоты, то ПЧ сам измеряет мощность и сохраняет это значение в одном из своих параметров
- С шильдика электродвигателя списываем его КПД и вычисляем мощность на валу PВ. На шильдике, конечно, указана и номинальная мощность электродвигателя, но в данном случае нас интересует мощность электродвигателя в рабочей точке насоса
- Если между двигателем и насосом существует жёсткая механическая связь (а не ременная передача, редуктор или муфта с проскальзыванием), то считаем потребляемую насосом мощность РП равной мощности на валу электродвигателя РВ
- Измеряем перепад давления на напорном и всасывающем патрубках и вычисляем напор (если необходимо, то корректируем его с учётом разницы диаметров и высот напорного и всасывающего патрубков)
- Измеряем расход и рассчитываем гидравлическую мощность насоса РГ
- Вычисляем КПД насоса.
Если КПД насоса оказался ниже, чем вы ожидали, то стоит задуматься о профилактике, ремонте или замене насоса.
Источник статьи: http://www.maxplant.ru/article/pump_efficiency.php
Основы гидравлики
Решение задач по гидродинамике
На этой странице приведена подборка несложных задач по гидродинамике жидкостей и теплотехнике, которые могут быть использованы для текущего контроля освоения дисциплины студентами.
К каждой задаче прилагается вариант решения с ответом.
Следует отметить, что решение большинства подобных задач возможно с использованием разных способов и алгоритмов, поэтому приведенные примеры решений не являются эталоном. Тем не менее, при разных методах решения задачи, результат решения (ответ) должен быть одинаковым.
Задача
Определить скорость движения жидкости в подводящей линии и скорость поршня, если известны:
- диаметр трубопровода d = 0,012 м;
- диаметр поршня D = 0,07 м;
- подача насоса Q = 1,7х10 -3 м 3 /с.
Потери напора в местных сопротивлениях не учитывать.
Скорость движения жидкости в подводящей линии:
vж = Q/Sтруб = 4Q/πd 2 = (4×1,7×10 -3 )/(3,14×0,012 2 ) = 15,04 м/с.
где Sтруб = πd 2 /4 – площадь сечения трубопровода подводящей линии.
Скорость перемещения поршня:
vп = Q/Sп = 4Q/πD 2 = (4×1,7×10 -3 )/(3,14×0,07 2 ) = 0,44 м/с.
Ответ: скорость движения жидкости в подводящей линии – 15,04 м/с, скорость поршня – 0,44 м/с.
Задача
Определить режимы движения рабочей жидкости в питающей и отводящей линии гидропривода, изображенного на схеме в приведенной выше задаче.
Исходные данные:
Скорость движения жидкости в питающей линии v1 = 15,04 м/с;
скорость движения жидкости в отводящей линии v2 = 10,08 м/с;
вязкость жидкости v = 0,5×10 -4 м 2 /с;
диаметр трубопроводов d = 0,012 м;
критическое число Рейнольдса для рабочей жидкости равно Reкр = 2320.
Потери напора в местных сопротивлениях и трубопроводах не учитывать.
Числа Рейнольдса, характеризующее режим движения жидкости, определяется по формуле:
где:
v – скорость движения жидкости в трубопроводе;
d – диаметр трубопровода;
v – кинематическая вязкость жидкости.
Тогда для питающей и отводящей линии число Рейнольдса будет соответственно равно:
Re1 = v 1d /v = (15,04×0,012)/(0,5×10 -4 ) = 3610;
Re2 = v 2d /v = (10,08×0,012)/(0,5×10 -4 ) = 2419.
Так как, полученные числа Re1 и Re2 больше критического Reкр = 2320, то движение жидкости в обоих случаях будет турбулентным.
Ответ: в питающей и отводящей линии режим движения жидкости будет турбулентным.
Задача
Определить режим движения нефти в трубопроводе диаметром d = 400 мм при скорости движения v = 0,13 м/с.
Кинематическая вязкость нефти v = 0,3×10 -4 м 2 /с, критерий Рейнольдса для нефти, определяющий переход от ламинарного движения к турбулентному Reкр = 2000…2300.
Приведем исходные данные к системе единиц СИ: d = 0,4 м.
Чтобы определить режим движения нефти в трубопроводе, вычислим число Рейнольдса для данного диаметра труб и скорости потока:
Re = v d/v = 0,13×0,4/0,3×10 -4 = 1733.
Ответ: поскольку число Рейнольдса менее критического значения, движение нефти в трубопроводе будет осуществляться в ламинарном режиме.
Задача
В дне бака высотой H = 4 м проделано отверстие площадью S = 4 см 2 .
Бак наполнен водой доверху, при этом уровень воды поддерживается постоянным благодаря пополнению из водопровода.
Определите, какую подачу воды должен обеспечить водопровод, чтобы ее уровень в баке оставался неизменным.
Коэффициент расхода отверстия равен μs = 0,6.
Подача (расход) воды определяется произведением площади отверстия S на скорость v истекающей из отверстия струи, поскольку объем вытекающей из отверстия воды должен компенсироваться водой из водопровода.
При истечении воды из малого отверстия в баке с постоянно поддерживаемым напором скорость струи v может быть определена по формуле Торричелли:
v = μs √(2gH) (м/с),
где: g = 9,81 м/с 2 — ускорение свободного падения, Н = 4 м – напор (уровень отверстия).
Тогда, с учетом формулы Торричелли, получим требуемую подачу воды из водопровода:
Q = S v = S μs √(2gH) = 4×10 -4 ×0,6 √ (2×9,81×4) ≈ 2,126×10 -3 м 3 /с ≈ 2,1 л/с.
Ответ: требуемый расход воды из водопровода примерно равен 2,1 л/с.
Задача
Вода вытекает из бака через конический сходящийся насадок с минимальным пропускным сечением S = 2 см 2 в ведро емкостью V = 10 л.
Коэффициент расхода насадка μs = 0,96.
Уровень воды в баке поддерживается постоянным от водопроводной сети.

Определить время t заполнения ведра водой.
При истечении жидкости из насадка при постоянном напоре объемный расход определяется по формуле:
где: g = 9,81 м/с 2 — ускорение свободного падения.
Приведем исходные данные к системе единиц СИ ( S = 0,0002 м 2 , V = 0,01 м 3 ), и, подставив известные величины в формулу, получим:
Q = μs S√(2gH) = 0,96×0,0002× √ (2×9,81×1,2) ≈ 0,00093 м 3 /с.
Чтобы определить время заполнения ведра водой необходимо объем ведра разделить на полученный объемный расход жидкости:
Ответ: ведро наполнится водой через 10,75 секунд.
Задачи по расчету параметров насосов
Задача
При частоте вращения вала 1000 мин -1 центробежный насос потребляет 4 кВт энергии, подает 20 литров воды в секунду под напором 10 метров.
Определить, как изменятся рабочие параметры насоса, если частоту вращения вала увеличить до 3000 мин -1 .
Зависимость рабочих параметров насоса от частоты вращения вала выражается уравнениями:
т. е. при увеличении частоты вращения вала насоса в три раза, его подачу, напор и потребляемую мощность можно определить по формулам:
Ответ: при увеличении частоты вращения до 3000 мин -1 подача насоса составит 60 л/с, напор – приблизительно 17,3 м, а потребляемая мощность – приблизительно 11,95 кВт.
Задача
Определите, какова объемная подача двухцилиндрового поршневого насоса, если диаметр его поршней d = 0,1 м, рабочий ход поршней l = 0,1 м, частота вращения вала приводного электродвигателя n = 960 мин -1 .
Объемные потери не учитывать.
Объемная подача поршневого насоса может быть определена, как рабочий объем всех его цилиндров, умноженный на количество рабочих циклов за единицу времени.
Частота вращения вала насоса n = 960 мин -1 = 16 с -1 , т. е. за одну секунду двухцилиндровый насос совершает 2×16 рабочих циклов (каждый цилиндр за один оборот совершает 1 цикл).
Рабочий объем одного цилиндра: Vц = l πd 2 /4 (м 3 ).
Тогда объемная подача насоса (без учета потерь) при данной частоте вращения составит:
Q = 2×16×l πd 2 /4 = 2×16×0,1×3,14×0,1 2 /4 = 0,02512 м 3 /с.
Ответ: объемная подача насоса составляет чуть более 25 л/с.
Задача
Определить диаметр поршней d аксиально-поршневого насоса, если известны параметры:
- диаметр окружности, на которой размещены поршни D = 80 мм;
- количество поршней в насосе z = 6;
- угол наклона диска (шайбы насоса) к оси цилиндров γ = 45˚;
- подача насоса Q равна 0,001 м 3 /с при частоте вращения вала n = 50 с -1 .
Подача аксиально-поршневого насоса определяется по формуле:
С учетом того, что tg γ = tg 45˚ = 1, а диаметр D в системе единиц СИ равен 0,08 м, выразим и определим из этой формулы диаметр поршней d :
d = √(4Q/πznD tg γ) = √ (4×0,001/3,14×6×50×0,08×1) ≈ 0,0073 м ≈7,3 мм.
Ответ: диаметр поршней насоса приблизительно равен 7,3 мм.
Задача
Определите, какую мощность должен иметь электродвигатель привода водяного насоса, если насос при подаче Q = 0,05 м 3 /с создает напор Н = 40 м, а его полный КПД η = 0,6.
Плотность воды принять равной ρ = 1000 кг/м 3 .
Полезная мощность любого насоса может быть определена по формуле:
где g = 9,81 м/с 2 – ускорение свободного падения.
Потребляемая мощность Nп , т. е. мощность, которую на работу насоса затрачивает электродвигатель Nэд (без учета потерь в приводе), равна полезной мощности с учетом КПД:
Nэд = Nп/η = ρgQH/η = 1000×9,81×0,05×40/0,6 = 32700 Вт = 32,7 кВт.
Ответ: для обеспечения работы насоса в заданном режиме
необходим электродвигатель мощностью 32,7 кВт.
Задача
Привод водяного насоса обеспечивает частоту вращения его вала n1 = 15 с -1 , при этом подача насоса составляет Q1 = 0,01 м 3 /с, а напор H1 = 20 м.
Определите, какова должна быть частота вращения вала насоса, если потребуется увеличить его напор до 80 м.
Как изменится при этом подача насоса?
Зависимость рабочих параметров насоса от частоты вращения его вала выражается уравнениями:
т. е. для увеличения напора в четыре раза, частота вращения вала насоса должна возрасти в два раза:
В соответствии с первой формулой, при увеличении частоты вращения вала насоса в два раза его подача тоже возрастет в два раза, и составит Q2 = 0,02 м 3 /с.
Ответ: для увеличения напора до 80 м (т. е. в четыре раза)
вал насоса должен вращаться с частотой 30 с -1 , при этом подача насоса возрастет в два раза.
Задача
Определите по приведенной здесь графической характеристике поршневого насоса, какова будет потребляемая им мощность и полный КПД, если подача равна 0,52 л/с.
Какое давление в системе при этом насос развивает?
Охарактеризуйте форму кривой, отображающей график зависимости Q = f(p) .
При подаче Q = 0,52 л/с насос потребляет мощность примерно равную 1,2 кВт, его КПД составляет 0,65 (максимальное значение).
Давление в системе при этом равно 1,6 МПа.
Зависимость подачи насоса от давления в системе отображает кривая Q = f(p) , которая показывает, что с нарастанием давления в системе подача уменьшается, при этом резкий спад величины подачи начинается при увеличении давления от точки на графике, характеризующей максимальный КПД насоса.
Скачать задачи по гидравлике с вариантами решений
(в формате Word, размер файла 324 кБ — 27 задач с решениями и вопросы по насосам)
Источник статьи: http://k-a-t.ru/gidravlika/zadachi_2/index.shtml